研究一下炮台旋转

使用环境参考

CocosCreator v3.8.7

前情提要

说某天深夜，游戏开发群里突然传来一声哀嚎——“救命啊！我的炮塔疯了！”

原来是某位苦逼的塔防游戏开发者，正抓耳挠腮地盯着屏幕：他精心设计的炮台，此刻正像个喝多了的醉汉，一会儿摇头晃脑转得飞快，一会儿又像被点了穴似的突然卡住，偶尔还会唰地一下 360 度大回环，活像在表演某种诡异的机械舞。

“我用 tween 做的索敌旋转，怎么就成了抽风现场？”他欲哭无泪地发问。

我一拍大腿：“兄弟，这实时追踪的活啊，就像谈恋爱——得时刻保持关注才行！tween 这种计划赶不上变化的方式，哪能应付战场上瞬息万变的敌人？听我一句劝，把旋转逻辑放进 update 里，让炮台和敌人来个你走一步，我跟一步的浪漫追踪吧！”

于是，就有了这篇研究笔记…

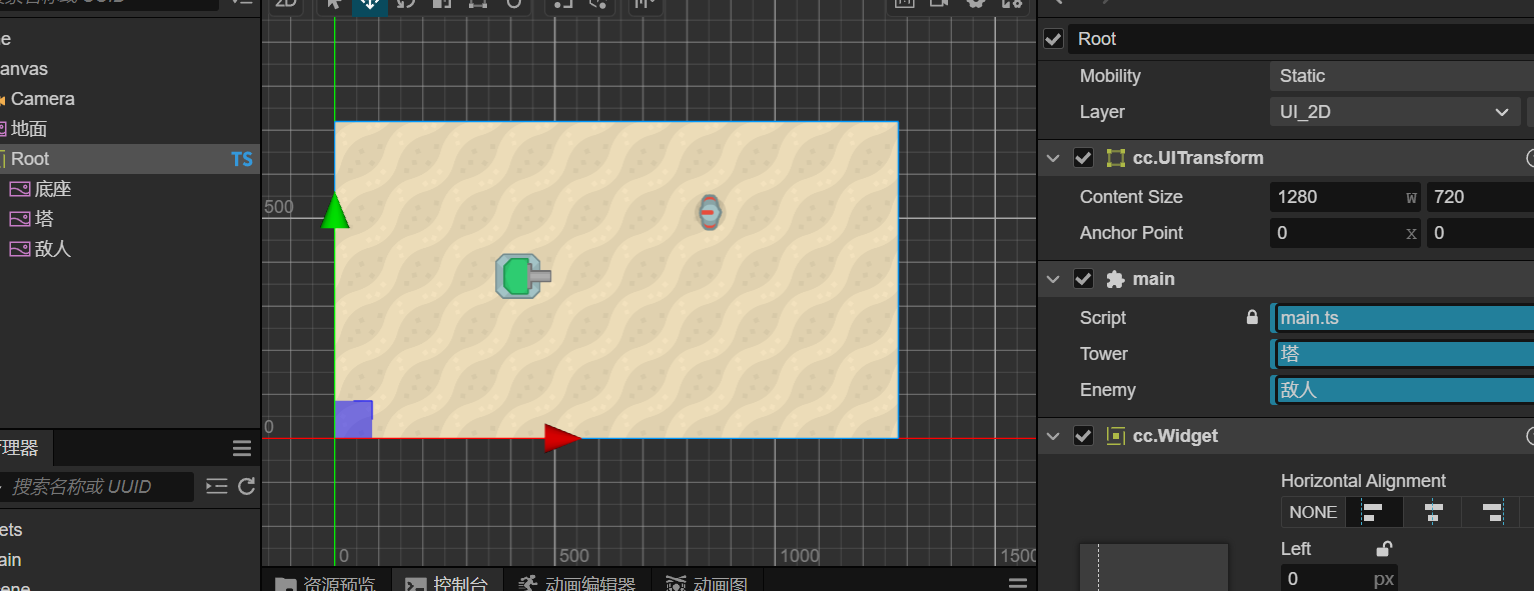
塔防大众做法

利用敌人位置与炮台位置计算差值，取 atan 弧度转角度，然后赋值给炮台的 angle 属性即可。

以下为项目代码：

import { _decorator, Component, EventMouse, Input, input, Node, v3 } from 'cc'
const { ccclass, property } = _decorator

@ccclass('main')
export class main extends Component {
  @property(Node) tower: Node
  @property(Node) enemy: Node

  start() {
    input.on(
      Input.EventType.MOUSE_MOVE,
      (event: EventMouse) => {
        if (event.getButton() === EventMouse.BUTTON_LEFT) {
          // 按住左键移动 enemy
          const delta = event.getUIDelta()
          this.enemy.translate(v3(delta.x, delta.y, 0))
        }
      },
      this
    )
  }

  update(deltaTime: number) {
    const dx = this.enemy.position.x - this.tower.position.x
    const dy = this.enemy.position.y - this.tower.position.y
    const radian = Math.atan2(dy, dx)
    const angle = (radian * 180) / Math.PI
    console.log(angle)
    this.tower.angle = angle
  }
}

角度环绕问题

如果直接赋值，是没问题的！但是，经常上战场的朋友们都知道，炮塔不会瞬间旋转到目标角度，而是会有一个旋转时间，这个缓动效果可以通过插值来实现。

update(deltaTime: number) {
  const dx = this.enemy.position.x - this.towerposition.x
  const dy = this.enemy.position.y - this.towerposition.y
  const radian = Math.atan2(dy, dx)
  const angle = (radian * 180) / Math.PI
  const interpolatedAngle = lerp(this.tower.angle, angle, deltaTime * 2)
  this.tower.angle = interpolatedAngle
}

然后出现了角度环绕问题！因为角度是一个循环值，在越过临界值时，会有“反向插值”情况出现。

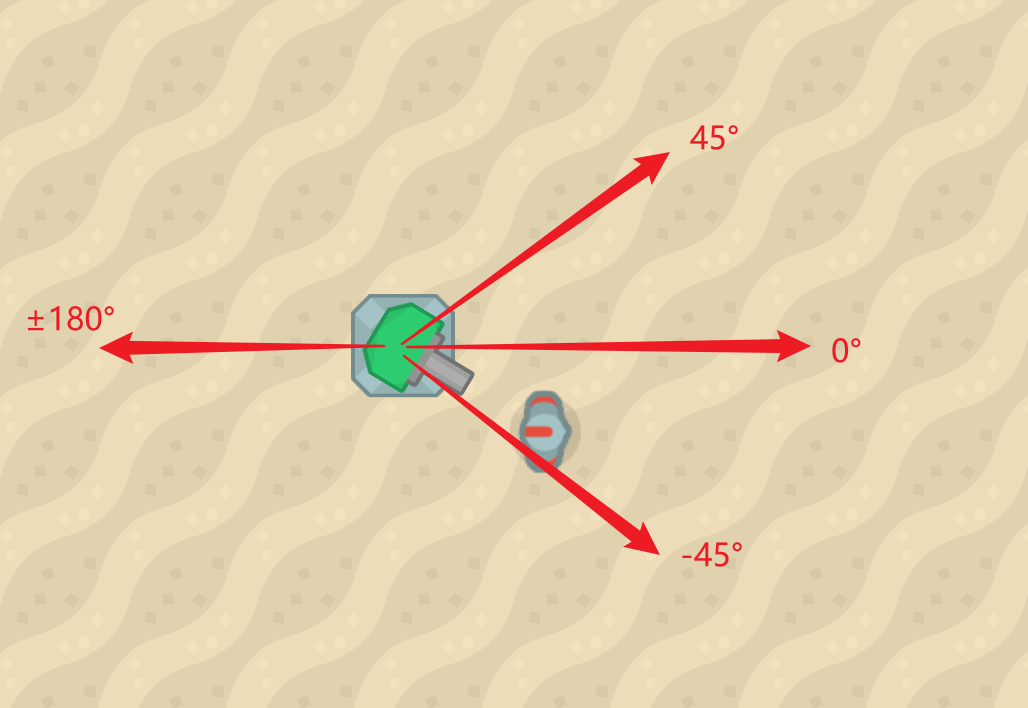
想解决这个问题，需要在计算角度差时，确保选择最短路径，即如果目标角度与当前角度相差超过 180 度，就选择反向旋转。

update(deltaTime: number) {
  const dx = this.enemy.position.x - this.tower.position.x
  const dy = this.enemy.position.y - this.tower.position.y
  const radian = Math.atan2(dy, dx)
  let angle = (radian * 180) / Math.PI

  // 计算角度差并确保选择最短路径
  let currentAngle = this.tower.angle
  let angleDiff = angle - currentAngle
  // 处理角度环绕问题
  if (angleDiff > 180) {
    angle -= 360
  } else if (angleDiff < -180) {
    angle += 360
  }

  const interpolatedAngle = lerp(this.tower.angle, angle, deltaTime * 2)
  this.tower.angle = interpolatedAngle
}

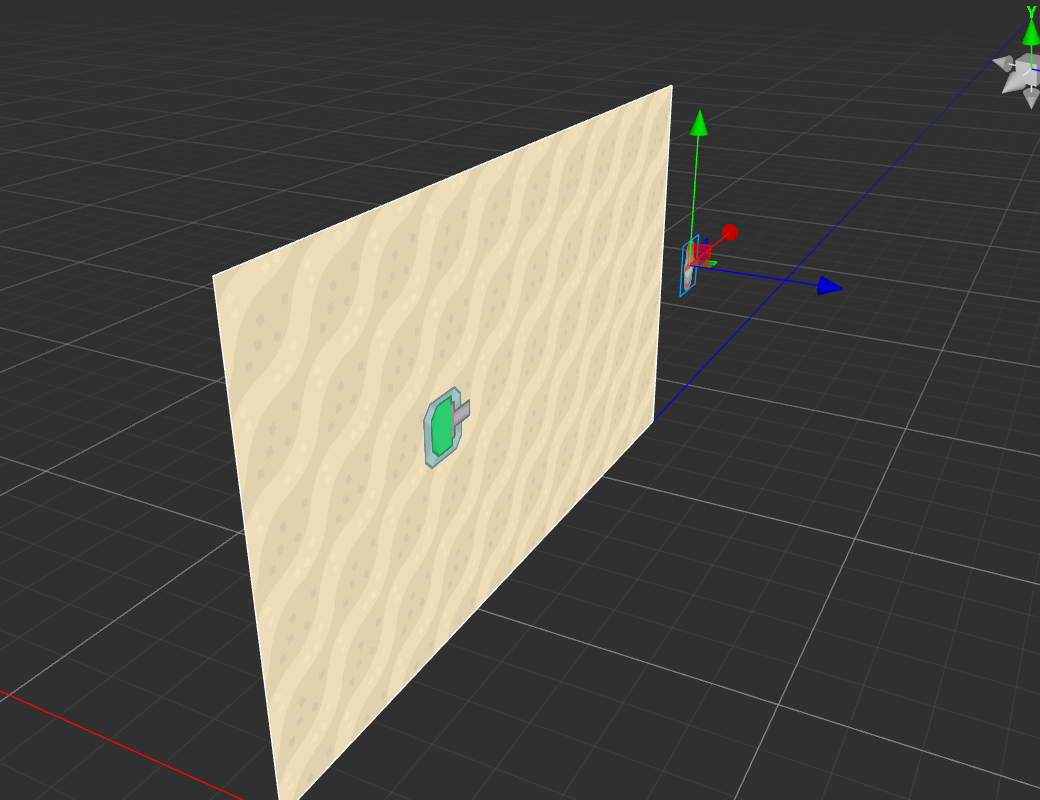
尝试三维方案

代码到这里其实已经把问题解决了！可咱程序员骨子里就藏着股“作妖”劲儿，这二维的玩法都搞定了，三维空间你不试试？

不过啊，三维旋转这事儿可不像二维那么简单！要是还用老办法，把 XYZ 三个角度分别单独计算差值再插值，那炮台虽然最终能到达目标角度，但是旋转路径会变得复杂跳脱，不够平滑。

四元数（Quaternion）是一种用于表示三维空间旋转的高效数学工具。在 CocosCreator 中 Rotation 就是四元数，它能够有效避免欧拉角旋转中常见的“万向节锁”问题！用一个简单的类比来理解：想象一个由三个同心圆环组成的陀螺仪，每个圆环分别对应一个旋转轴。当中间的 Y 轴圆环旋转 90 度时，最内层和最外层的 XZ 轴圆环会完全对齐，此时无论再绕哪个轴旋转，效果都会变成同一个方向的旋转，就像锁死了一样！

四元数在插值计算中表现更为平滑，而且有内置的 Quat 类方法来方便计算，代码如下：

我把敌人“飞”高一些，有 Z 值。

update(deltaTime: number) {
  // 使用三维空间计算方式
  const dV3 = this.enemy.getPosition().subtract(this.tower.getPosition())
  // 归一化方向向量
  const normalizedDir = dV3.normalize()
  // 创建目标四元数
  const targetQuat = quat()
  // 这里的 1,0,0 向量是炮塔的起始方向，targetQuat 就是炮塔需要旋转到的目标，这里是提前计算
  Quat.rotationTo(targetQuat, v3(1, 0, 0), normalizedDir)
  // 获取当前塔的旋转四元数
  const currentQuat = this.tower.getRotation()
  // 创建插值四元数来存储结果
  const slerpedQuat = quat()
  // 使用球面线性插值（SLERP）来平滑旋转
  // 第三个参数是插值因子，值越大旋转越快
  Quat.slerp(slerpedQuat, currentQuat, targetQuat, deltaTime * 2)
  // 应用插值后的旋转到塔上
  this.tower.setRotation(slerpedQuat)
}

总结

瞄准，开炮！

我是阔阔，一位喜欢研究的程序员！

个人网站：www.kuokuo666.com

2025！Day Day Up！